Tortoise and Hare Guidance: Accelerating Diffusion Model Inference with Multirate Integration

Yunghee Lee

Byeonghyun Pak

Junwha Hong

Hoseong Kim ^†

Agency for Defense Development

Accepted to NeurIPS 2025

^†Corresponding author

Paper Code

Abstract

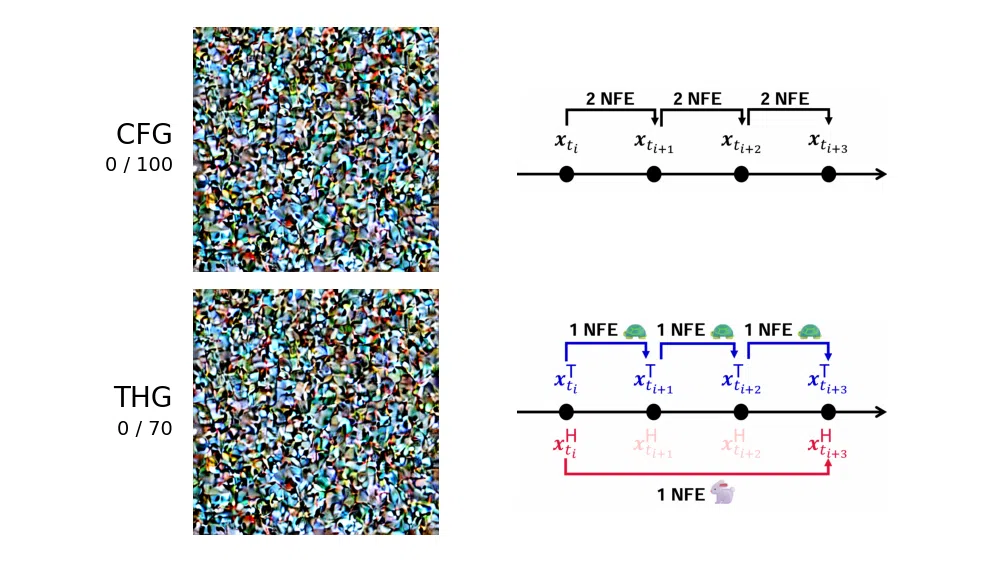
In this paper, we propose Tortoise and Hare Guidance (THG), a training-free strategy that accelerates diffusion sampling while maintaining high-fidelity generation. We demonstrate that the noise estimate and the additional guidance term exhibit markedly different sensitivity to numerical error by reformulating the classifier-free guidance (CFG) ODE as a multirate system of ODEs. Our error-bound analysis shows that the additional guidance branch is more robust to approximation, revealing substantial redundancy that conventional solvers fail to exploit.

Building on this insight, THG significantly reduces the computation of the additional guidance: the noise estimate is integrated with the tortoise equation on the original, fine-grained timestep grid, while the additional guidance is integrated with the hare equation only on a coarse grid. We also introduce (i) an error-bound-aware timestep sampler that adaptively selects step sizes and (ii) a guidance-scale scheduler that stabilizes large extrapolation spans.

THG reduces the number of function evaluations (NFE) by up to 30% with virtually no loss in generation fidelity (∆ImageReward ≤ 0.032) and outperforms state-of-the-art CFG-based training-free accelerators under identical computation budgets. Our findings highlight the potential of multirate formulations for diffusion solvers, paving the way for real-time high-quality image synthesis without any model retraining. The source code is available at https://github.com/yhlee-add/THG.

Method

Diffusion model inference can be viewed as an initial-value ODE problem. Given classifier-free guidance (CFG) $\hat{\epsilon}_\theta (x_t) = \textcolor{mediumblue}{\hat{\epsilon}_c (x_t)} + \textcolor{crimson}{(\omega-1)\cdot \Delta\hat{\epsilon}_c (x_t)}$ , we cast the diffusion ODE $\frac{\mathrm{d}x_t}{\mathrm{d}t} = f(t) x_t + \frac{g^2(t)}{2\sigma_t} \hat{\epsilon}_\theta (x_t)$ as a two-state multirate system of ODEs

\def\xT{\textcolor{mediumblue}{x_t^\mathsf{T}}} \def\xH{\textcolor{crimson}{x_t^\mathsf{H}}} \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \xT &= f(t)\xT + \frac{g^2(t)}{2\sigma_t} \textcolor{mediumblue}{\hat{\epsilon}_c (\xT + \xH)}, \\ \frac{\mathrm{d}}{\mathrm{d}t} \xH &= f(t)\xH + \frac{g^2(t)}{2\sigma_t} \textcolor{crimson}{(\omega-1)\Delta\hat{\epsilon}_c (\xT + \xH)}. \end{aligned}

Since the additional guidance term varies more slowly w.r.t. the denoising timestep

t

than the noise estimate term, we apply a multirate integration scheme that uses a coarser timestep grid for the additional guidance term. Also, we perform an approximation error-bound analysis to determine the appropriate grid granularity and propose an adaptive guidance scale to compensate for any performance degradation.

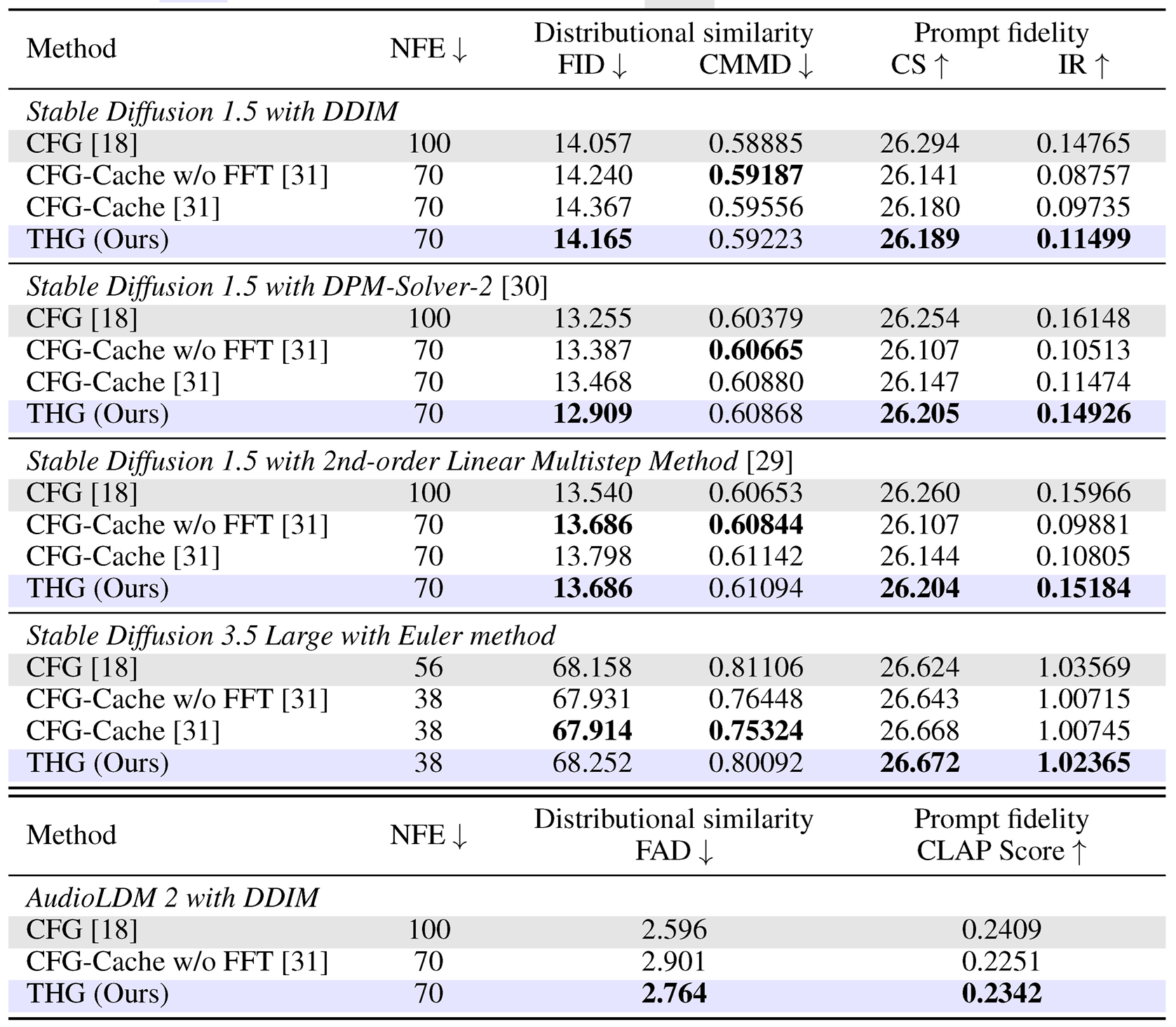
Comparison with Existing Methods

Comparison of methods in terms of distributional similarity and prompt fidelity. — THG generalizes across solvers and scales, preserving generation quality under aggresive NFE reduction.

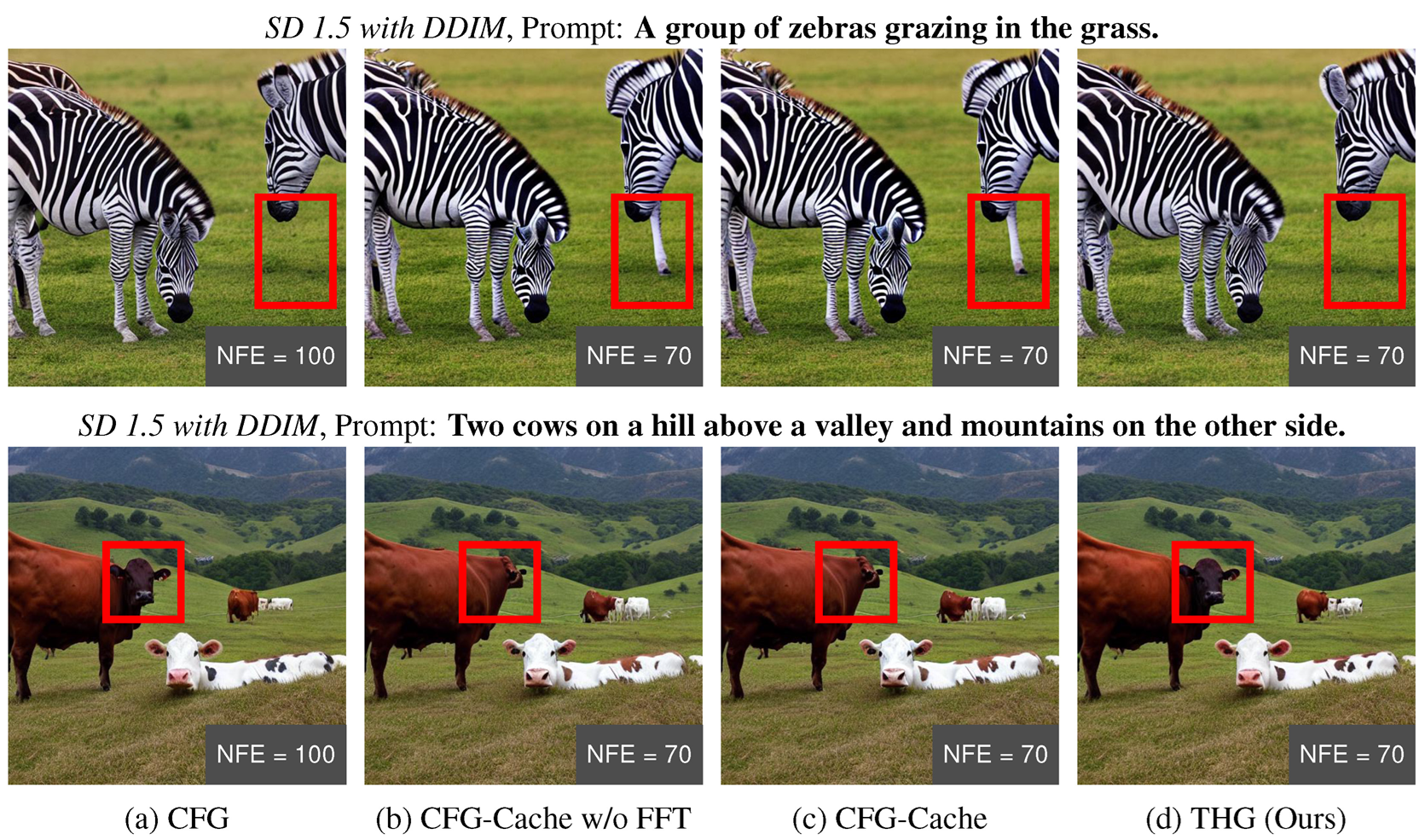
Visual Comparison

Comparison of images generated by different methods. — THG effectively preserves image fidelity and fine details.

BibTeX citation

@inproceedings{
  lee2025tortoise,
  title={Tortoise and Hare Guidance: Accelerating Diffusion Model Inference with Multirate Integration},
  author={Yunghee Lee and Byeonghyun Pak and Junwha Hong and Hoseong Kim},
  booktitle={The Thirty-ninth Annual Conference on Neural Information Processing Systems},
  year={2025},
  url={https://openreview.net/forum?id=3cYcUmcDhU}
}